Romb je pojam koji potiče iz grčkog jezika i najjednostavnije se prevodi kao – iskošeni kvadrat. Termin romba je zastupljen u geometriji i predstavlja četvorougao koji pripada vrsti paralelograma.
Romb ima sve stranice jednakih dužina, a karakteristično za njega je proizvoljna veličina ugla koji se nalazi između dve njegove strane, i ona može da se menja u realnom intervalu. Posebna vrsta romba, kome su stranice normalne jedna drugoj, se naziva – kvadrat.
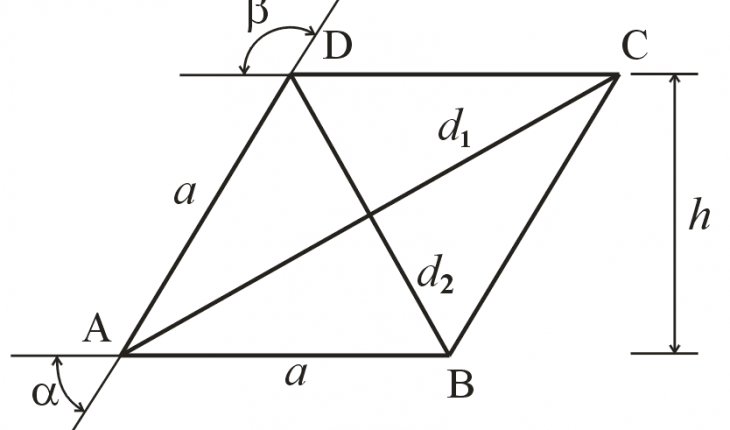
Romb sadrži sledeće elemente: temena (A, B, C, D), dužine stranica (a), visinu (h), dijagonale (d1, d2) i uglove (α i ß). Naspramni uglovi romba su jednaki, što znači da postoje samo dve različite veličine uglova između strana romba (α i ß). Zbir uglova u četvorouglu određuje vrednost veličine drugog ugla (samo ukoliko je prvi poznat), te je tako romb određen samo sa dužinom stranice i jednim uglom. Uglovi između dijagonala su jednaki i iznose 90˚.
Romb se sastoji od sledeće teoreme:
- Romb predstavlja paralelogram i samim tim ima sve osobine paralelograma.
- Prave koje imaju dijagonale romba su osi simetrije.
- Dijagonale romba su normalne i polove uglove romba.
Presek dijagonala romba predstavlja centar upisane kružnice. Romb, inače, nema opisanu kružnicu, sem kvadrata koji je poseban slučaj romba, koji ima sve prave uglove.
Površina romba se može izračunati preko dijagonala – ako su dijagonale romba d1 i d2 , onda je formula za izračunavanje površine romba : P = d1 x d2 / 2. Takođe, površina romba se može izračunati i preko stranica, kao i površinom paralelograma, iz razloga što je romb ujedno i paralelogram. Tada je, površina romba jednaka dvema površinama trouglova stranice kojima su strane jednake. Površina romba se može izračunati i uz pomoć vrednosti njegove visine (h), a formula glasi: P = a x h, gde “a” označava dužinu stranice romba.
Pitagorina teorema je našla svoju primenu i kod romba, jer ona važi za pravougli trougao, a romb se sastoji od trouglova. Pitagorina teorema glasi – “ Kvadrat nad hipotenuzom je jednak zbiru kvadrata nad katetama” pravouglog trougla. U slučaju kada je dužina stranica romba nepoznata, mogu se izračunati pomoću ove teoreme, s’ tim da je dužina dijagonala romba poznata. Tada će se kvadrat stranice romba izračunati na osnovu sledeće formule: a2 = (d1 / 2) 2 + (d2 / 2), gde je “a” – osnovica romba, d1 – dužina dijagonale romba, d2 – kraća dijagonala romba.